DDPG & TRPO

DDPG : Test

Deterministic Policy Gradient Theorem

이 글은 Gabriel Peyré, Marco Cuturi의 Computational Optimal Transport를 읽고 단순히 이해 가는대로 번역한 내용이다.

???: 번역인데 왜 영어가 더 많나요?

Theoretical Foundations of OT

이번 장에서는 optimal transport의 기본 개념에 대해 설명한다. 먼저, 확률 벡터 $(\mathbf{a}, \mathbf{b})$ 사이의 optimal matching과 coupling에 대해 소개하며, 이 계산을 discrete measures로 부터 arbitrary measures의 일반적인 설정으로 일반화한다.

1. Histograms and Measures

$\mathbf{a} \in \Sigma_n$의 모든 원소에 대해, histogram과 probability vector라는 용어를 구분 없이 사용할 것이다. 여기에서, $\Sigma_n$은 probability simplex로 다음과 같이 정의한다.

$\Sigma_n$: probability simplex with $n$ bins, namely the set of probability vectors in $\R_{+}^{n}$ \(\Sigma_n \coloneqq \biggl\{ \mathbf{a} \in \R_{+}^{n} \colon \sum_{i=1}^{n}{\mathbf{a}_i} = 1 \biggr\}\)

---

Remark 1. Discrete measure.

A discrete measure with weights $\mathbf{a}$ and locations $x_1, \cdots, x_n \in \mathcal{X}$ reads

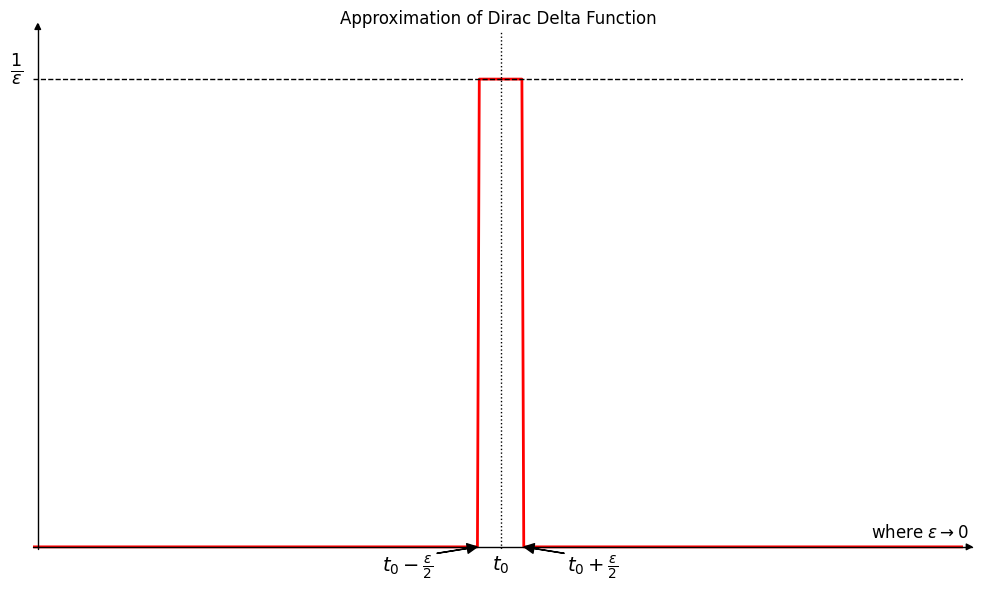
\[\alpha = \sum_{i=1}^n \mathbf{a}_i\delta_{x_i}\]

where $\delta_x$ is the Dirac at position $x$.

---

Dirac delta는 위 그림처럼 생겼다. 미분방정식 배울때 봤던 기억이 있는데(기억안남), 지금 생각해보면 kronecker delta를 극한의 개념을 통해 연속적인 형태로 바꾼 것 같다. Dirac $(\delta_x)$을 간단히 표현하면, \(\delta_x \simeq \begin{cases} +\infty, & x = 0\\ 0, & x \neq 0 \end{cases}\) 이다.

이 관점에서, 위의 식

\begin{equation} \label{eq1} \begin{split} A & = \frac{\pi r^2}{2}
& = \frac{1}{2} \pi r^2 \end{split} \end{equation}